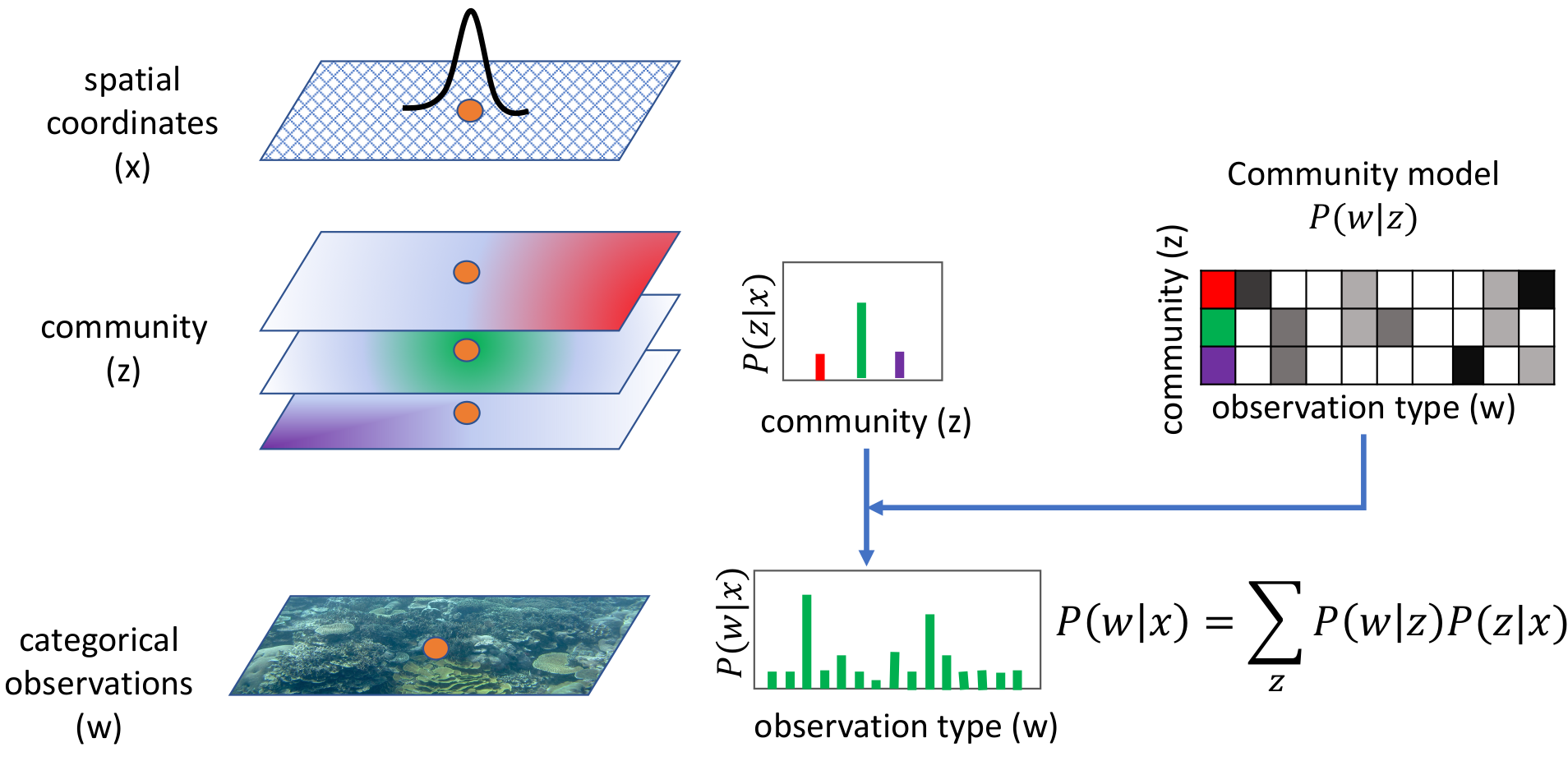
Categorical observations, such as observations of phytoplankton taxa, are factored into the product of a community model and spatiotemporal distributions for each community. The community model, which is the distribution of taxa in each community, is modeled with a Dirichlet prior; and the spatial distribution of each community is modeled using a Gaussian process.

We propose a generative model for the spatio-temporal distribution of high dimensional categorical observations. These are commonly produced by robots equipped with an imaging sensor such as a camera, paired with an image classifier, potentially producing observations over thousands of categories. The proposed approach combines the use of Dirichlet distributions to model sparse co-occurrence relations between the observed categories using a latent variable, and Gaussian processes to model the latent variable's spatio-temporal distribution. Experiments in this paper show that the resulting model is able to efficiently and accurately approximate the temporal distribution of high dimensional categorical measurements such as taxonomic observations of microscopic organisms in the ocean, even in unobserved (held out) locations, far from other samples. This work's primary motivation is to enable deployment of informative path planning techniques over high dimensional categorical fields, which until now have been limited to scalar or low dimensional vector observations.

Soucie, J. S., Sosik, H., & Girdhar, Y. (2020). Gaussian-Dirichlet Random Fields for Inference over High Dimensional Categorical Observations. [To appear in] International Conference on Robotics and Automation (ICRA).
[ArXiv Preprint]